Today’s post will actually build on last week’s post about decomposing fractions. Building a solid foundation for fractions in the upper elementary grades is essential for supporting students’ understanding of operations with fractions in the middle grades. Last week, I discussed how important it is for students to be able to compose and decompose fractions. This week, I will extend this understanding to addition and subtraction stories.
Specifically, this activity address the following Common Core State Standard for Math:
4.NF.B.3.D- Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
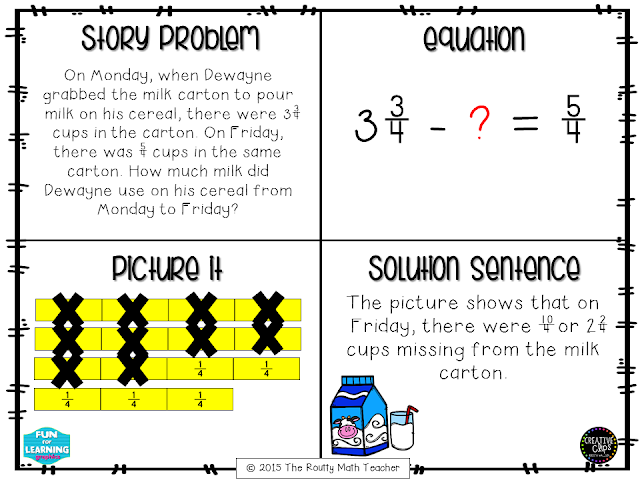
The illustration below shows how to represent and make sense of the story problem displayed below.
Requiring students to use multiple representations to represent the story will support the students’ understanding of the connection between the verbal story, equation, and visual model. Depending on the interpretation of the verbal story, the equation and visual model may not be represented the way we might expect them to be. However, using multiple representations provides a strong foundation for the work to be done in middle and high school.
When solving word problems, it is important for students to understand what story is being told. The Common Core State Standards for Math describe addition and subtraction of fractions as the joining and separating of parts. With this definition in mind, when we read the story problem in the picture above, we see that there was an initial amount of milk and then a part of the container was separated (removed), leaving a specific amount of milk in the carton.
To write the problem as subtracting five-fourths from three and three-fourths misinterprets the problem. Writing an equation that matches the situation will help students understand how to make sense of the pictorial model and their solution. In the example above, notice that the pictorial model shows all parts removed except for the five-fourths that remained. This allows students to see that the part we need to find is the change from the initial amount to the leftover amount.
It is important to note that this problem could be rewritten with the same numbers and the same context but the interpretation be different. What if Dewayne started with three and three-fourths cups of milk and drank five-fourths cups of them? It’s a worthwhile exploration to do with students because many of them would have incorrectly assigned the equation for the situation above to the solution in the illustration above.
As a general rule, when it comes to word problems, be sure to ask your students, “What story is the word problem telling?” Then encourage students to match their equations and visual models to their interpretation of the problem. Being able to successfully interpret the problem allows students to choose a model that correctly fits the situation and will lead to a successful response.
